(중학교수학 중학수학) 삼각형의 내각

일본 명문 중학교 입시수학: 도형비법: 마에다 타쿠로오 손민영 옮김

삼각형 ABC가 있습니다.

BC와 평행하고 A를 지나는 직선 DE를 긋습니다.

중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학

BC//DE이므로

각DAB = 각ABC (엇각)

각EAC = 각ACB (엇각)

각BAC = 각BAC (자기자신)

===============더하면

(각DAB + 각BAC + 각CAE) = 각ABC + 각BCA + 각CAB

여기서 우변의 세 각은 삼각형의 세 내각이므로 우변의 값이 세 내각의 합입니다.

좌변의 세 각은 직선DE에서 A를 중심으로 나눠진 세 각이므로 그 합은 직선, 즉, 180도입니다.

따라서 삼각형의 세 내각의 합은 180도입니다.

삼각형의 내각과의각의뜻

삼각형의 안쪽과 바깥쪽입니다. 예를 들어 정삼각형은 한각에 60도인데 그 바깥쪽은 120도입니다.

삼감형의 합동의뜻

특정한 삼각형과 모양이 완전히 같은 삼각형입니다.

이등변삼각형과 정삼각형의뜻

이등변삼각형은 삼각형의 세변중에 두변의 길이가 같다는 겁니다.

정삼각형은 세각,세변의 길이가 모두 같은 도형입니다.

삼각형의 내각의 합이 180도라고 하는 것은 한바퀴가 360도로 정해 져있기 때문에 나온 것이지 누가 주장해서는 아니라고 생각이 듭니다.

삼각형의 각각의 꼭지점을 오려서 한군데로 모아 보시면 180도가 됩니다. 즉 반바퀴이죠. 그래서 한바퀴의 각도를 정하는 것이 우선이라고 보여 집니다.

한바퀴는 60분법에 의한 각도로 360도 입니다.

아래의 글은 60분법의 유래 입니다. 참고하세요.

60분법이란 말그대로 60으로 나눈다는 말입니다.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
하지만 무엇을 60으로 나눌까요?
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
그것은 원을 60으로 나누는 것이 아니라 도(˚)를 60으로 나눈다는 말입니다.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
도(˚) 아랫 단위를 분('), 그 아랫단위를 초('')라고 하죠.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
1도(˚)는 60분('), 1분(')은 60초('')가 되는 것입니다.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
참고로 도(°)는, 직각의 1/90로 정의되고, 분과 초를 사용하는 이유는 각도의 분수사용을 피하기 위해서 입니다.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
분수를 사용하면 여러가지로 불편해지겠죠.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
그리고 원을 360으로 나누게된 이유는 360이라는 수가 많은 정수로 떨어지기 때문으로 추측된다고 합니다.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
원을 360으로 나누어 쓰게된 기원이 워낙 오래전이고 고대로 부터 널리 쓰여져 지금으로선 추측만 할 수 있을 뿐이죠.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
360의 약수는 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360 등입니다.

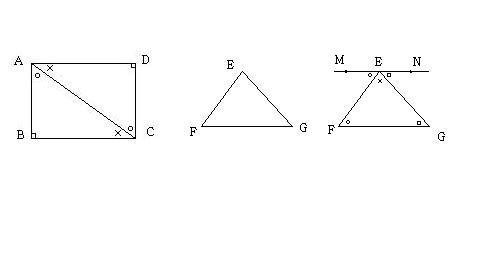
( 1 )

위 그림 □ABCD 가 있습니다. 먼저 사각형의 내각의 총합은 360˚ 입니다.

□ABCD 에 선분 AC를 그어봅시다.

직사각형의 성질에 의해 선분 AB // DC 이므로, ∠BAC = ∠DCA (엇각)

마찬가지로 선분 AD // BC 이므로, ∠DAC = ∠ACB (엇각)

따라서, 두 삼각형은 합동이죠 .△ABC ≡ △ CDA

□ABCD 에서, 90 + 90 + O + X + O + X = 360˚ 입니다.

정리해보면,

2(90 + O + X) = 360˚

90 + O + X = 180˚

위 결과에 의해, .△ABC 의 내각의 합은 180˚ 입니다.

( 2 )

두번째 오른쪽의 .△EFG 를 봅시다.

E점을 지나며, 선분 FG와 평행하게 직선MN을 그어보면,

평행선의 성질에 의해, ∠MEF = ∠EFG (엇각) , ∠NEG = ∠EGF (엇각)

O + X + ㅁ = 180˚ (평각) 입니다.

따라서, .△EFG 의 내각의 합은 .180˚ 입니다.

결과적으로, 두 조건 (1), (2) 에 의해서 삼각형의 내각의 합은 180˚ 가 됩니다.

그러니까

일단 반으로 자른 두 삼각형의 높이는 같습니다

그러니까 밑변만을 따지는 거죠

그래서!!!

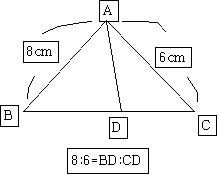
내각의 이등분선 성질이 AB:AC=BD:CD라는 거에 대입해 보면

8:6=BD:CD

밑변BD:CD의 비도 8:6인 거죠

그러니까 넓이의 비는 8:6인데 약분해서 4:3

4+3는 7이고 전체 넓이는 21입니다.

나누면 1은 3제곱센티미터인데

삼각형 ABD는 비가 4였기 때문에

3곱하기 4로

12제곱센티미터가 되는 겁니다.

네 궁금하신점은

'어떻게 이런 식이 나왔냐?'

라는 것인데

이 문제에서 밑변의 길이와 높이는 주어지지 않았습니다.

이 높이와 밑변은 구하지 못하죠

그렇게 때문에 비가 있는겁니다.

제가쓴 3과4도 비입니다.

일단 두 삼각형 ABD와ADC는

높이가 같으니 이건 고려하지 않아도 됩니다.

밑변BD 와 밑변DC는

8:6의 비 (절대로 길이가 아닙니다.)

가 있는겁니다.

8:6을 모두 더하면 14

14로는 21을 나눌수 없기 때문에

비를 약분해서 4:3 (2로 나눔)

이 되는거고요

그럼 넓이의 비도

4:3이 되는겁니다.

그리고 4+3는

7입니다.

21을 7로 나눔니다.

그럼 2이 됩니다.

그럼 비 중 구하려는

삼각형 ABD는 비가 4이므로

3을 곱해서 12가 되는거죠

아니면

8-나를 하신다면 웬만한 방정식을 배우셨을 것이고

그래서 방정식으로 하자면 으로 하자면

일단 ABD등등 쓰기가 어려우니까(귀차니즘)

ABD는 a / ADC는 b로 하는거죠

식1----- 4:3=a:b --------3a=4b

식2----- a+b=21 -------b=21-a

식1에 식2를 대입하면

4(21-a)=84 - 4a

= > 3a=84 - 4a

7a=84

a=12=ABD

그래서 삼각형 ABD는 12가 되는겁니다.

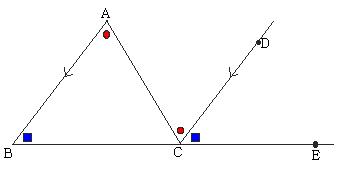
삼각형 ABC에 대하여 C를 지나면 선분 AB와 평행한 직선CD를 긋자.

그러면 선분 AB와 선분 CD가 평행하므로 동위각과 엇각의 크기가 같다.

즉, (동위각)-----(1), 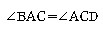(엇각)--------(2)

이때, 각C의 외각의 크기는 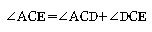이고 (1)과 (2)에 의해

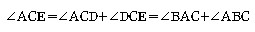이 성립한다.

따라서, 삼각형의 한 외각의 크기는 이와 이웃하지 않는 두 내각 합과 같다.

[결론] 선분AD가 각A의 이등분선일 때 AB:AC=BD:CD

[증명]

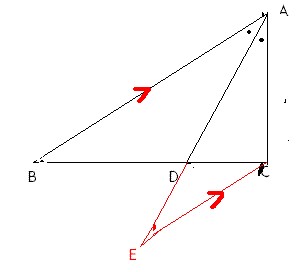
다음과 같이 선분AD의 연장선을 긋고 점C에서 선분AB와 평행하게 선분을 긋습니다.

만나는 교점을 E 라고 하면

△ABD∽△ECD(AA닮음)

따라서

선분AB:선분EC=선분BD:선분CD ........ (1)

또한 ∠BAE = ∠CEA (엇각) 이고

△CEA 에서 ∠BAE = ∠CEA (두 밑각의 크기가 같으므로) 이등변삼각형 따라서

선분AC = 선분EC ..... (2)

위에 비례식에서 선분EC 대신에 선분 AC 를 대입할 수 있다.

(2) 를 (1)에 대입하면

선분AB: 선분AC =선분BD:선분CD

1. 두 평행선을 그리고
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
한 평행선 위의 한 점과 다른 한 평행선 위의 두 점을 이어서 삼각형을 만들어요
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
그리고 두 점을 포함한 평행선 위의 각중 하나를 잡고, 연장된 선 위에 있는 각을 생각해 보아요. 그 두 각의 합은 180도 이죠? 직선이니까요.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
그럼 이 각이 아닌 다른 두 각을 생각해 볼께요.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
두 점을 포함한 평행선 위의 각중 다른 각은 한 점을 포함한 평행선 위의 점의 바깥깍에 대해 엇각으로 같고 그 엇각과 삼각형 내의 각의 합은
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
저 위에 연장된 선 위에 있는 각과 크기가 같으므로
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
삼각형의 세 각의 합은 180도가 됩니다.
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
2. 임의의 삼각형을 그렸을 때 그 삼각형의 세 점을 꼭지점으로 하는 평행사변형을 그릴 수 있지요? 그 평행사변형을 ABCD라고 했을 때 인접한 두 각의 합은 언제나 180도이지요? (연장선으로 그어보면 한 각은 엇각이 되니까요.)
중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학 중학교수학 중학수학
그러면 대각선을 하나 그립니다 대각선에 의해 나누어진 각을 살펴보면 서로 엇각으로 삼각형의 다른 각이 대각선으로 나뉜 각이 이등분 되고 난 각이 됨을 알 수 있죠.? 따라서 이 두각과 나머지 한 각을 더하면 180도가 됩니다.^^

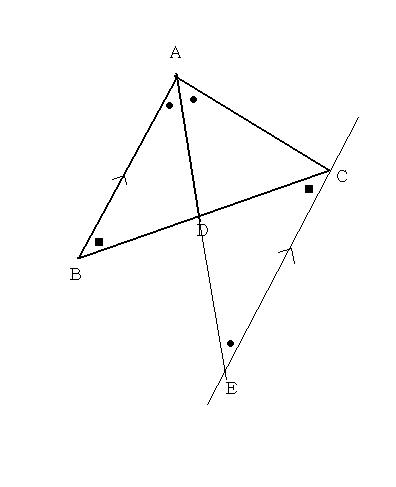
그림 참고해주세요^^

점 C를 지나고 선분 AB에 평행한 직선과 , 선분AD의 연장선과 만나는 교점을 E라 하면

∠BAD = ∠DEC

∠ABD= ∠DCE

(그림은 좀 이상하지만 ) △CAE는 이등변 삼각형이므로 선분 AC와 선분 CE는 같다.

그리고 △DAB∽△DEC 이므로

선분 AB : 선분 CE = 선분 BD : 선분 CD

선분 CE는 선분 AC와 같으므로

따라서 선분 AB : 선분 AC = 선분 BD : 선분 CD 입니다^^

저작자표시

'DirectX > 수학/물리' 카테고리의 다른 글

속도와 속력 (0)	2010.07.19
게임수학과 물리 - 1행렬 (0)	2010.06.10
게임수학과 물리 - 1벡터 (0)	2010.06.09
http://www.viper.pe.kr/cgi-bin/moin.cgi/TitleIndex (0)	2010.06.09
삼각함수~ (0)	2010.06.09

(중학교수학 중학수학) 삼각형의 내각

'DirectX > 수학/물리' 카테고리의 다른 글

'DirectX/수학/물리' Related Articles

티스토리툴바