directx의 파이프라인을 따라 구현하기 위해 우선 필요한 것은
벡터와 행렬이다.
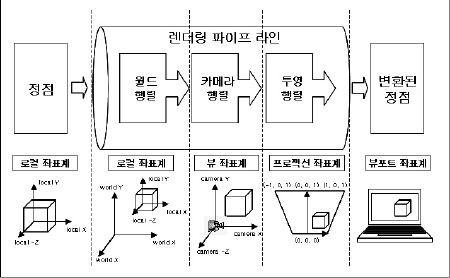
파이프라인은 위와 같은 방법으로 진행이 된다.
우선 일반적인 물체를 구현한다. 이 물체는 자신을 기준으로 한 좌표계를 가진다.
이것이 모델 좌표계이다.
여러 모델들, 즉 여러 물체를 한 곳에서 관리하기 위해 전체틀을 제공하는 것이
월드 좌표계이다. 월드좌표계를 사용하여 현재 좌표계에 속한 모든 물체를 한번에 돌리거나
이동이 가능하다. dx에서의 월드좌표계를 구현해 본다.
우선 이전에 구현해둔 벡터와 행렬을 dx에 맞게 바꾼다. 이전 버전은 opengl형식을 따르므로
이동행렬, 회전행렬을 적절히 설정해 주어야 하며 행렬의 곱하는 순서를 바꾸어 주어야 한다.
dx랜더링 대신 dibsection을 사용한 bitblt를 사용하며 전반적인 과정은 dx의 순서를 따른다.
1. 메인에서의 윈도우 클래스 등록
WNDCLASSEX wc = { sizeof(WNDCLASSEX), CS_CLASSDC, MsgProc, 0L, 0L,
GetModuleHandle(NULL), NULL, NULL, NULL, NULL, "Mgun Tutorial", NULL };
RegisterClassEx( &wc );
HWND hWnd = CreateWindow( "Mgun Tutorial", "Mgun Graphics",
WS_OVERLAPPEDWINDOW, CW_USEDEFAULT,CW_USEDEFAULT,CW_USEDEFAULT,CW_USEDEFAULT,
GetDesktopWindow(), NULL, wc.hInstance, NULL );
ShowWindow(hWnd,SW_SHOWNORMAL);
2. 초기화 단계 - 물체 및 버퍼 설정
이 단계에서 정점버퍼나 인덱스버퍼, 또는 화면설정에 대한 초기설정을 해 준다.
이 부분에서 고민점들은 아래와 같았다.
- 각 물체들의 모델 위치는 따로 설정을 해 주어야 하는가?
일반적으로 모든 물체는 버텍스(점)으로 이루어진 삼각형의 조합이다.
즉, 임의로 큐브객체를 만든다고 해도 그것은 일반적인 점의 집합을 인덱스에 맞게
그어 만든 삼각형이다. 즉, 큐브객체를 따로 만들어 자동으로 생성한다 해도 이는 사실
내부에 점들을 한꺼번에 찍어주는 역활만을 한다. 그래서 이를 따로 이동,회전변환등을
위한 기능을 심어주지는 않는다.
- 그리는 방법은?
후에 있을 cw, ccw등을 고려해서 각 점들은 인덱스버퍼에 설정된 대로 그려진다.
dx의 개념인 버텍스버퍼와 인덱스 버퍼가 기본적으로 각 물체내에 설정되어져 있다.
- 화면의 영역은?
화면의 영역은 원하는 크기만큼 설정하여 dibsection에서 설정한다.
3. 랜더링 단계 - PeekMessage
GetMessage가 아닌 PeekMessage를 사용한다. 이 차이는 예전에 올린 글에 자세히 설명되어져 있다.
다만 하드웨어 가속에 따른 cpu 상태를 위해 Sleep함수를 이용하여 cpu점유율 상태를 완화시켜준다.
WNDCLASSEX wc = { sizeof(WNDCLASSEX), CS_CLASSDC, MsgProc, 0L, 0L,
GetModuleHandle(NULL), NULL, NULL, NULL, NULL,
"Mgun Tutorial", NULL };
RegisterClassEx( &wc );
/// 윈도우 생성
HWND hWnd = CreateWindow( "Mgun Tutorial", "Mgun Graphics",
WS_OVERLAPPEDWINDOW, CW_USEDEFAULT,CW_USEDEFAULT,CW_USEDEFAULT,CW_USEDEFAULT,
GetDesktopWindow(), NULL, wc.hInstance, NULL );
if(SUCCEEDED(Initialize(hWnd)))
{
ShowWindow( hWnd, SW_SHOWDEFAULT );
UpdateWindow( hWnd );
MSG msg;
ZeroMemory(&msg, sizeof(msg));
while(msg.message != WM_QUIT)
{
Sleep(5);
if(PeekMessage(&msg, NULL, 0U, 0U, PM_REMOVE))
{
TranslateMessage(&msg);
DispatchMessage(&msg);
}
else
Render();
}
}
return 0;
[출처] DX 파이프라인 따라하기. [1. 창생성] (비공개 카페)
기본적인 변환에는 이동, 회전, 크기변환이 있고 투영(Projection)변환과 카메라(Viewing)변환,
반사(Reflection)과 전단(Shearing)등이 있으며 이들의 변환이 3D 애니메이션을 제공한다.
컴퓨터그래픽스에서는 이들 모든 변환을 행렬(Matrix)로 표시하여 연산한다.
행렬은 Vector을 움직이는 시스템이기 때문이며 행렬이 없었다면 3D Graphics라는 장르가
생기지도 않았을지 모른다.
특히 역행렬, 곱셈행렬의 연산속도는 무척 빠르다.
이전 글에서는 기본적인 틀을만들었다.
이번에는 파이프라인의 월드변환을 알아본다.
월드변환은 로컬좌표로 표시된 여러개의 오브젝트를 월드좌표계로
통일하여 좌표변환을 실시한다.
이를 위해 각 오브젝트는 신축/회전/이동의 변환을 수행하게 되며
만약 애니메이션이 있다면 애니메이션 행렬도 여기에 결합된다.
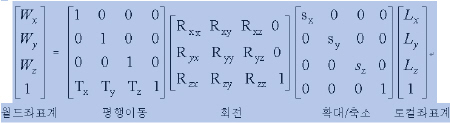
즉, 위와 같은 순서로 곱하여 진다. 일반적으로 이를 SRT 라고 한다.
위의 순서를 그대로 적용해 큐브를 위한 8개읨 점을 찍고 이에 행렬변환을 적용해보았다.
//cube의 월드행렬 설정전의 로컬 위치 설정.
cubeMatrix.Identity(); //step1. 초기화
cubeMatrix.Scale(1); //step2. 신축 (S)
cubeMatrix.XRotate(30); //step3. 회전 (R)
cubeMatrix.Translate(100,0,0); //step4. 이동 (T)
그리고 월드행렬을 만든다.
matWorld.Identity();
device.MatrixRotationY(matWorld, GetTickCount()/30.0f);
matWorld = cubeMatrix * matWorld;
월드행렬에 원하는 변환을 하고 큐브에 행해준 변환과 곱한다.
[출처] DX 파이프라인 따라하기. [2. World 변환] (비공개 카페)
뷰 변환은 시점을 고려하여 월드 전체를 사람이 보는 각도에 맞도록 변환하는 것이다.
컴퓨터 3D 그래픽스는 반드시 일정한 시점에서 오브젝트를 본 것만 렌더링해야 하기 때문이다.
이 카메라 행렬은 또한 기저 벡터변환(x y z축 자체 변환)을 해야 한다.
고려해야 할 점.
1. 나(eye)는 어디에 있는가 - 시점, 뷰위치, 뷰공간원점이라 불린다.
2. 나는 어디(lookat)를 바라보고 있는가. - 뷰 방향벡터
3. 머리 위쪽 - 기준점이 된다. - 하나의 벡터를 가지고 정렬하는 방향들의 무한한 개수가 존재하기 때문에
뷰 방향벡터만으로는 부족하다, 가능성을 하나로 제한하기 위해 뷰업벡터가 필요하다.
그리고 뷰업벡터와 직교인 두번째 벡터를 지정하는데 이는 뷰 사이드 벡터또는 카메라의 오른쪽
벡터라고 한다.
세개의 뷰 벡터들은 월드안에 표현되며 서로 직교이기 떄문에 정규화 함으로써 정규직교 기저를 생성할 수 있다.
일반적으로 z축을 뷰 방향 벡터로, y축을 뷰업벡터로, x축을 뷰 사이드벡터로 사상한다.
카메라의 위치를 Eye, 카메라가 보고 있는 점 LookAt, 지면에서 수직방향 up을 가지고
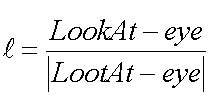
카메라 시선 방향벡터 (방향은 바뀌어도 길이가 변하지 않도록 정규화함)
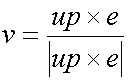
카메라 옆 방향벡터(수직 방향 up와 시선벡터 l에 직교하는 우측벡터)
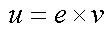
이제 카메라 상방벡터(시선벡터 l와 옆방향벡터 v에 직교하는 카메라 상방벡터)를 구할 수 있다.
이 e,v,u가 새로운 좌표계에서 xyz축 방향 단위벡터가 되므로 새로운 좌표계로의 기저변환 벡터가 된다.
일반적으로 카메라 위치는 월드좌표계에서 (0,0,=1) 에 있으며 카메라의 시선방향은 z축(원점)에 두고
카메라의 위 방향을 y축으로 한다.
이제 카메라 좌표계에서는 카메라의 위치가 원점에 있어야 하며 월드 좌표계에서 카메라의 위치가
C = (Cx, Cy, Cz)라면 평행이동의 역행렬로 처리된다.
위를 코드로 구현한 부분은 아래와 같다.
void Device::MatrixLookAtLH(Matrix& v, Vector3& eye, Vector3& look, Vector3& up)
{
Matrix temp;
Vector3 vD, vR, vU; //월드 벡터.
up.Normalize();
vD = look - eye; //눈과 물체사이의 거리를 나타내는 거리벡터 - z축
vD.Normalize();
vR.Cross(up,vD); //업과 거리를 외적시켜 만든 사이드 벡터 - x축
vR.Normalize();
vU.Cross(vD,vR); //사이드(x)와 거리(z)를 외적시켜 만든 업벡터 - y축
temp.m_Element[0][0] = vR.m_data[0];
temp.m_Element[1][0] = vR.m_data[1];
temp.m_Element[2][0] = vR.m_data[2];
temp.m_Element[0][1] = vU.m_data[0];
temp.m_Element[1][1] = vU.m_data[1];
temp.m_Element[2][1] = vU.m_data[2];
temp.m_Element[0][2] = vD.m_data[0];
temp.m_Element[1][2] = vD.m_data[1];
temp.m_Element[2][2] = vD.m_data[2];
temp.m_Element[3][0] = -(eye.Dot(vR));
temp.m_Element[3][1] = -(eye.Dot(vU));
temp.m_Element[3][2] = -(eye.Dot(vD));
temp.m_Element[3][3] = 1.0f;
v *= temp;
}
위의 코드는 뷰변환을 위한 행렬을 만들어 준다.
matView.Identity();
Vector3 vEyePt(0.0f, 10.0f, -450.0f); //camera position
Vector3 vLookatPt(0.0f, 0.0f, 0.0f); //point looking at
Vector3 vUpVec(0.0f, 1.0f, 0.0f); //up vector
device.MatrixLookAtLH(matView, vEyePt, vLookatPt, vUpVec);
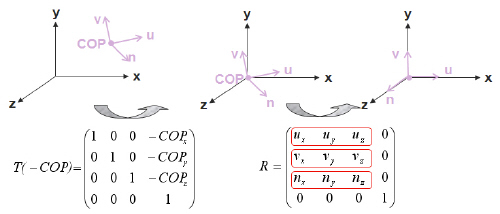
위의 그림은 뷰변환에 대한 이해를 돕기 위한 그림이다.
다만 위의 행렬식은 OpenGL의 양식을 따르므로 Dx방식으로 바꾸고싶다면 전치행렬처럼
만들어 주면 된다.
즉, T의 이동값을 [0][3],[1][3],[2][3] 번째요소에 넣는 것이 아니라 [3][0],[3][1],[3][2]에 넣는다.
R역시 u,는 0번째 열에 , v는 1번째 열에, n은 2번째 열에 넣는다.
이를 곱한 값이 뷰변환을 위한 행렬이 된다.
[출처] DX 파이프라인 따라하기. [3. View 변환] (비공개 카페)
투영 변환은 3차원 좌표계(카메라 좌표계)를 2차원 좌표계로 변환하는 것을 말한다.
투영에는 직교투영과 원근투영이 있다. 직교투영은 3차원 좌표중 z값을 0으로 만든 경우로서
정밀 모델링에 사용되나 현실감이 떨어진다.
원근 투영은 거리에 따라 물체의 크기와 모양이 변하는 것을 표현하는 것으로 게임제작용으로
많이 사용된다.
[예] 카메라 주름 상자
초,중등 시절에 자주 실험을 하던 바늘구멍상자를 기억하는가?
누군가 태양이 환히 비치는 날에 어두운 방에 들어갔는데 거기에 태양광의 일부가 그 방으로
들어올 수 있도록 해주는 작은 구멍이 있다고 가정해 보자.
비록 상하와 좌우가 바뀌었겠지만 바깥 세상의 이미지를 디스플레이하도록 그 빛은 방의 반대편 벽 위에
투영될 것이다. 이것이 핀홀 사진기가 작동할 수 있도록 해주는 동일한 원리이다.
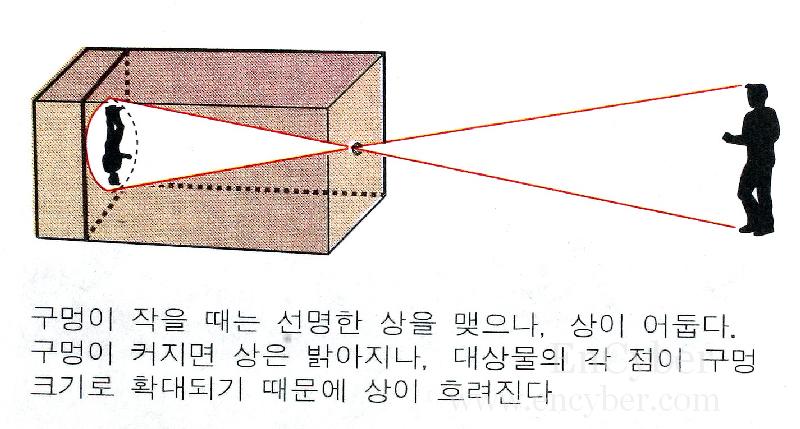
즉 그 구멍이 렌즈의 초점과 같은 동작을 한다.
이러한 경우에 모든 투영의 선들은하나의 투영의 중심을 통과한다.
임의의 점이 원본 점과 투영의 중심 모두를 통과하는 선을 구성해서 그것이 투영의 평면 어디를 교차하는지를
계산함으로써 그 평면 위의 어디로 변환되는지를 결정할 수 있다.
투영에서 이러한 순서를 원근투영(perspective projection)이라고 한다.
평행투영은 일관성을 보장한다.
멀리있는것, 가까이있는것을 고려하지 않고 항상 동일한 크기를 보여준다.
이는 실제감을 반감시키지만 정밀한 건축설계시에 자주 사용되어 진다.
평행투영은 뷰 평면과 수직일 경우 정사영, 수직이 아닐경우 사선투영이라고 불린다.
무한한 뷰 평면을 디스플레이 장치에 사상하는 것은 불가능하다.
대신에 뷰 윈도우를 설정하는데 이것이 장치에 사상될 뷰 평면 위에 사각영역의 틀을 잡는다.
공간은 6개의 평면들로 지정된 볼록 부피로 제한하고 이 안에 모든것이 랜더링 될 것이고,
반대로 그것들의 외부에 있는 모든것은 제외된다.
이러한 영역 또는 부피를 뷰절두체 또는 뷰 부피라고한다.
절두체
절두체란, 뷰포트의 카메라에 대해서 상대적으로 배치된 장면(scene)내의 3D 볼륨이다. 이 볼륨의 형상은,카메라 공간으 로부터 스크린에 모델을 투영 하는 방법으로 영향을 준다. 가장 일반적인 투영은, 퍼스펙티브 투영이다. 이 투영에서는, 카메라의 근처에 있는 개체가, 카메라의 멀리 있는 개체보다 크게 표시된다. 퍼스펙티브 뷰의 경우, 절두체와는 첨단에 카메라가 있는 피라미드라고 생각하면 알기 쉽다. 이 피라미드는, 앞쪽 및 뒷쪽 클립면과 교차한다. 앞쪽과 뒷쪽 클립면과의 사이에 있는 피라미드내의 입체가 절두체이다. 개체는, 이 입체내에 있을 때에만 볼 수가 있다.

절 두체는, 어두운 방 중(안)에서 정방형의 창으로부터 밖을 보고 있는 상황을 상상 하면 알기 쉽다. 별도인 표현을 하면, 앞쪽 클립면은 창이며, 뒷쪽 클립면은 시야를 최종적으로 차단하는 것, 예를 들어, 거리의 고층빌딩, 먼 곳의 산맥, 또는 완전한 무의 공간이다. 절두체의 내부 (창으로부터 최종적으로 차단하는 것까지의 사이)에 있는 것은 모두 볼 수가 있어 그 이외의 것은 볼 수가 없다.
절두체는, z 좌표로 지정되는 앞쪽 및 뒷쪽 클립면의 사이의 거리와 FOV (시야)로 정의된다.

투영 행렬이란, 일반적으로, 스케일링과 원근법에 따르는 투영이다. 투영 변환에서는 절두체를 입방체에 변환 한다.
절두체의 가까이의 구석은 먼 구석보다 작기 때문에, 이 변환에는 카메라의 가까이의 개체를 확대한다고
하는 효과가 있어, 이것에 의해 장면(scene)에 원근감이 태어난다.
절두체에서는, 뷰 변환 공간의 원점과 카메라의 사이의 거리가 임의의 값 D 로서 정의되어 투영 행렬은 다음과 같이 된다.

뷰 행렬은, z 방향으로 D 만 평행이동 하는 것에 의해, 카메라를 원점에 평행이동 한다. 평행이동 행렬은, 다음과 같이 된다.

평행이동 행렬에 투영 행렬을 곱셈 (T*P) 하면, 그것들을 합성한 투영 행렬이 생긴다. 이것은 다음과 같이 된다.

다음 그림은 퍼스펙티브 변환이 절두체를 새로운 좌표 공간으로 변환하는 방법을 나타내고 있다. 절두체가 입방체가 되는 것, 및 장면(scene)의 우상각에 있던 원점이 중심으로 이동하는 것에 주목한다.

퍼스펙티브 변환에서는, x 방향과 y 방향의 한계는 -1 과 1 이다. z 방향의 한계는,
앞쪽면 도착해 0 으로, 뒷쪽면에 대해서는 1 이다.
이 행렬은, 카메라로부터 앞쪽의 클립면까지의 거리에 근거해 개체를 평행이동 및 스케일링 한다.
그러나, 이 행렬은 시야 (FOV)를 고려하지 않고, 먼 개체에 대해서 생성하는 z 값은 거의 같아서,
깊이 비교가 곤란하게 된다. 이 문제를 해결하기 위해서, 다음의 행렬은,
뷰포트의 어스펙트비(가로세로 비율)을 고려해 정점을 조정해,
어스펙트비(가로세로 비율)을 퍼스펙티브 투영에 맞춘다.

이 행렬에서는,Zn 는 앞쪽의 클립면의 z 값이다. 변수 w,h,Q 의 의미는, 다음과 같다.
fovw 및 fovk 는, 뷰포트의 수평 방향 및 수직 방향의 시야를 나타낸다 (라디안 단위).

애플리케이션에서는, 시야 각도를 사용해 x 와 y 의 배율을 정의하는 것은,
뷰포트의 수평 치수와 수직 치수 (카메라 공간의 것)를 사용하는데 비교해 불편한 경우가 있다.
수치 연산으로서 다음에 나타내는 w 와 h 용의 2 개의 식에서는 뷰포트의 사이즈를 사용하고 있다.
이러한 식은 위에의 공식과 동등하다.

이러한 식에서는,Zn 는 앞쪽의 클립면의 위치 좌표를 나타내, 변수 Vw 와 Vh 는 카메라 공간에서의
뷰포트의 폭과 높이를 나타내고 있다.
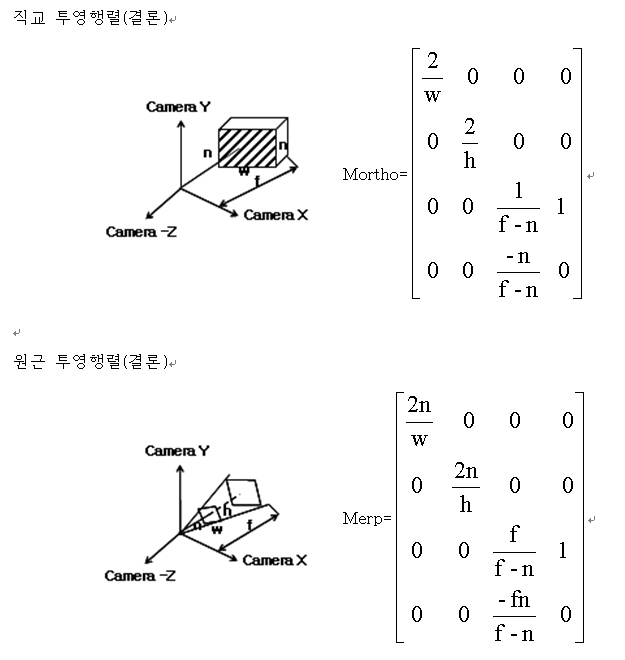
이를 구현하는 코드는 아래와 같다.
void Device::MatrixPerspectiveFovLH(Matrix& pOut, float fovY, float aspect, float zn, float zf)
{
Matrix temp;
float w,h,d;
w = 1.0f/tanf(fovY*0.5f);
h = 1.0f/(tanf(fovY*0.5f) * aspect);
d = zf / (zf-zn);
temp.m_Element[0][0] = w;
temp.m_Element[1][1] = h;
temp.m_Element[2][2] = d;
temp.m_Element[2][3] = 1;
temp.m_Element[3][2] = -(d*zn);
pOut *= temp;
}
현재 까지 물체들이 뷰 프레임 좌표계에 존재한다.
원점으로 뷰 윈도우의 중심을 사용할 것이고 뷰 윈도우의 변들에 정렬된 각각의 윈도우 넓이와 높이의 절반의
크기를 가지는 기저벡터들을 생성한다.
이러한 프레임 안에서 뷰 윈도우는 -1~1인 선들로 경계가 지워진 원점에 중심이 있는
2단위 크기를 가지는 정사각형으로 변환된다.
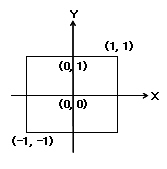
이것을 프레임으로 사용하는 것이 여러크기의 장치들로 사상할 때 어느정도 유연성을 제공한다.
직접 다양한 너비와 높이를 가질 수 있는 화면 여역으로 변환하는 것보다, 계산을 단순화하기 위해서
이러한 정규화된 형태를 중간단계로서 사용하고 그 다음 최종 단계로 화면 변환을 수행한다.
이러한 이유로 이 프레임 안의 좌표계를 정규화 장치 좌표계(NDC)라고 한다.
예전글에서 점과 벡터의 차이점을 이야기 할때 점은 네번쨰 성분 요소로 1을, 벡터는 0을 가진다고 하였다.
점은 동차공간에서(x,y,z,w)로 사상되고 w에 대한 표준값은 w로 세 좌표값을 나누면 (x/w, y/w, z/w, 1)이 된다.
w=0일때 이는 점이 아니라 벡터라 할수 있고 이것을 '무한히 멀리 있는 점'이라고 생각할 수 있다.
즉, w=0인 경우를 피하도록 노력해야하며 나눗셈을 수행하기 전에 이것을 조사하는 것이 현명하다.
[출처] DX 파이프라인 따라하기. [4. Projection 변환]-1 (비공개 카페)
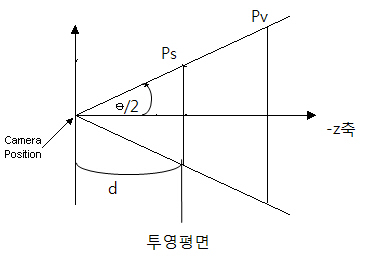
원근 투영 구성.
그림에서 가장 왼쪽에 있는 점이 투영중심[시점]이고 수직선이 뷰 평면이다.
뷰 절두체 평면들 중 하나위에 놓인 뷰 좌표계에서 점 Pv를 가지고 있고 뷰 평면위에 놓인 대응하는 점
Ps를 구하길 원한다고 가정해 보자.
Ps의 y좌표를 찾는 것은 간단하다.
윈도우의 상단에 부딪힐 때 까지 투영의 선이 그 평면을 따라가도록 한다.
뷰 윈도우의 높이가 2이고 0에 중점이 맞추어져 있기 때문에 Ps의 y좌표는 뷰 윈도우 높이의 절반인 1이 된다.
d는 어떻게 구할 수 있을까?
y뷰 절두체 평면들의 절단면은 투영의 중심으로부터 뷰 윈도우의 범위 (1,d),(1,-d)를 통과하는 선들로
표현될 수 있다. 이러한 선들 사이의 각도가 시야 fov이다.
이때 음의축 위에 놓인 영역만 고려함으로써 문제를 단순화할 수 있다.
즉, 시야를 fov/2의 각으로 이등분 하는 것이다.
z축과 Ps사이의 거리가 1이라는 것을 알기 때문에 1/d = tan( fov/2)로 설정할 수 있따.
이는 d = 1/tan(fov/2) 가 되며 이는 cot(fov/2)와 같다.
따라서 고정된 뷰 윈도우 크기에 대해서, 시야의 각을 알기만 하면 거리 d를 구할 수 있다.
위 방법으로 상단 뷰 절두체 평면위에 놓인 임의의 점에 대한 좌표를 구할 수 있다.
이러한 2D 절단면인 경우에 모든 점들이 하나의 점 (1,-d)로 투영된다.
마찬가지로 아래쪽 y 절두체 평면 위에 놓인 점들은 (-1,0d)로 투영될 것이다.
그렇지만 뷰 공간 안에 일반적인 점 (Yv,Zv)를 가지고 있다고 가정하자.
그것의 투영도 또한 뷰 평면 위에 놓일 것이라는 것을 알고 있기 때문에 Zndc좌표는 -d일 것이지만
Yndc는 어떻게 구할 수 있을까?
이것은 닮은꼴 삼각형을 사용해서 구해야 한다.
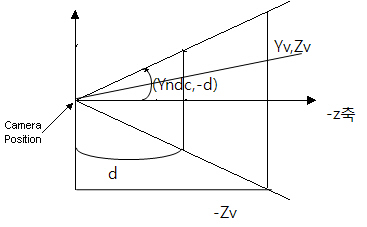
만약 임의의점 (Yv,Zv)를 가지고 있다면 그림에서 대응하는 직각 삼각형의 빗변의 길이가 Yv, 그리고
-Zv이다(-Z축을 바라보고 있으므로). 투영된 점의 경우에 직각 삼각형의 변들의 길이는 Yndc와 d이다.
닮은꼴 삼각형 이므로 다음을 얻는다.
Yndc/d = Yv/-Zv.
Yndc에 대해서 풀면 다음을 얻는다.
Yndc = dYv/=Zv
이것이 Y방향에서 좌표를 알려준다.
만약 뷰 영역이 정사각형이라면 x방향에 대해서도 같은 식을 사용할 수 있지만 대부분 그렇지 않다.
뷰 영역의 종횡비에 의해서 이것을 수정해야만 하며 이는 a = Wv/Hv로 정의 된다.
여기서 Wv와 Hv는 각각 뷰 사각형의 너비와 높이다. NDC뷰 윈도우 높이가 2이고 종횡비에 의해
NDC 뷰 너비를 수정한다고 가정할 것이다. 마찬가지로 닮은꼴 삼각형이므로 다음과 같은 공식을얻는다.
aXndc/d = Xv/-Zv
Xndc에 대해 풀면 Xndc = dXv/-aZv.
그래서 최종 투영 변환 공식은 다음과 같다.
Xndc = dXv/-aZv, Yndc = dYv/-aZv
여기서 주목해야 하는 것은 z좌표로 나눗셈을 수행한다는 것이다.
이로 인해 행렬 연산으로 전체 변환을 표현할 수 없다는 것이다.
이제 동차 공간에서 변환이 나와야 한다.
이를 위해서 w값으로 다른 좌표들을 나누어야만 한다.
만약 w값에 -Zv를 사상하도록 행렬을 설정한다면, 변환의 비선형적인 부분을 다루기 위해서
동차 나누기를 이용할 수 있다. 동차 나누기 이전에 그러한 상황을 일련의 선형 방정식들로
정리 할 수 있고 다음과 같다.
x = d/a * x
y = dy
z = dx
w = -z
4차원 선형 변환으로 이것을 다룰 수 있다.
기저벡터들을 살펴보면 e0가 (d/a, 0, 0, 0)으로 e1이 (0, d, 0, 0), e2가 (0,0,d,-1), e3가(0,0,0,0)으로
사상되는데, w가 이 공식 어디에도 사용되지 않는다.
이것에 근거한 동차 원근 행렬은 아래와 같다.
[ d/a 0 0 0 ]
[ 0 d 0 0 ]
[ 0 0 d 0 ]
[ 0 0 -1 0 ]
기대했던 것처럼 변환된 w값은 더이상 1이 아니다.
이 행렬의 가장 우측열이 0이므로 이 행렬은 역또한 가지지 않는다.
이것이 기대한 결과인데 정보의 한 차원을 잃어버리기 때문이다.
동일한 투영의 선을 따라 놓인 뷰 공간에서 개별적인 점들이 NDC공간에서 하나의 점으로 사상될 것이다.
따라서 NDC 공간에서 하나의 점이 주어진다면, 뷰 공간에서 그것의 원래 위치들을 재구성하는 것은 불가능하다.
실제 이 행렬이 어떻게 동작하는지 살펴보면, 만약 뷰 공간에서 일반적인 점에 이 행렬을 곱한다면
결과는 아래와 같다.
[ d/a 0 0 0 ] [x] [dx/a]
[ 0 d 0 0 ] [y] = [ dy ]
[ 0 0 d 0 ] [z] [ dz ]
[ 0 0 -1 0 ] [1] [ -z ]
이를 w로 나누면 다음과 같이 된다.
Xndc = dx / -az
Yndc = dy / -z
Zndc = -d
이것이 우리가 기대한 결과이다.
지금까지 x와 y를 투영하는 것을 다루어 왔고 z에 대해서는 완전히 무시했었다.
이전 유도과정에서 모든 z값들은 투영 평면에 거리의 음인 -d로 사상된다.
차원을 잃어버리는 것이 개념적으로 일리가 있지만 (결국 3D 공간에서 2D 평면으로 투영하므로) 실용적인
이유 때문에 z버퍼나 또 다른 깊이 비교를 위해서 z값들을 유지하는 것이 낫다.
뷰 윈도우 안에 X와 Y값들을 [-1,1]의 구간으로 사상할 것이므로, 마찬가지로 z값에 대해서
근단면과 원단면 위치안에 놓이도록 사상한다.
근단면과 원단면을 시점에상대적인 n과 f로 지정할 것이고 그래서 근단면 위에 놓인 점들은 -n인
Zv값을 가지고 -1인 Zndc값으로 사상된다. ( 참고로 Dx의 경우는 깊이에 대한 사상범위가 [0,1]이므로
Zndc가 0으로 사상된다.) 원단면 위에 놓인 그러한점들은 -f인 Zv값을 가지고 1로 사상될 것이다.
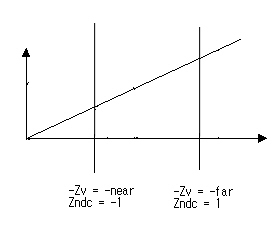
xy좌표들을 구하기 위해서 사용한 것과 약간 다른 방법으로Zndc에 대한 공식을 유도할 것이다.
구간 [-n, -f]를 [-1, 1]로 사상하기 위해서 두 가지 변환들이 존재한다.
첫번째 그 구간으로 그만큼 비례 축소하는 것이고 두번째는 그것을 [-1,1]로 이동하는 것이다.
통상적으로 이것은 일련의 선형 변환과정이지만, 최종적인 w 나눗셈과 같은 곤란한 문제가 있다.
대신에, 비례 축소와 이동 인자에 대한 미지수를 가진 원근 행렬을 만들 것이고
미지수들에 대해서 해를 구하기 위해서 -n과 -f에 대한 최종값들을 안다는사실을 사용할 것이다.
첫 원근행렬은 아래와 같다.
[ d/a 0 0 0 ]
[ 0 d 0 0 ]
[ 0 0 A B]
[ 0 0 -1 0 ]
여기서 A와 B는 각각 미지수인 비례 축소와 이동 인자들이다.
만약 근단면 위의 점 (0,0,-n)에 이 값을 곱한다면 다음과 같다.
[ d/a 0 0 0 ] [0] [0]
[ 0 d 0 0 ] [0 ] = [0]
[ 0 0 A B] [-n] [ -An + B ]
[ 0 0 -1 0 ] [1] [n]
w를 나누면 다음을 얻는다.
Zndc = -A + B/n
근단면 위의 임의의 점이 -1인 정규화된 장치 좌표로 사상된다는 것을 알고 그래서 Zndc에 -1을 대입해서
B에 대해서 풀수 있다.
B = (A-1)n
이제 원본행렬과 원단면 위의 임의의 점(0,0,-f)를 곱하는 것으로 대체하면 다음과 같다.
[ d/a 0 0 0 ] [0] [0]
[ 0 d 0 0 ] [0 ] = [0]
[ 0 0 A (A-1)n] [-f] [ -Af + (A-1)n ]
[ 0 0 -1 0 ] [1] [f]
그렇게 하면 다음과 같은 Zndc를 얻는다.
Zndc = -A + (A-1)n/f
=-A + A(n/f) - n/f
= A(n/f-1)-n/f
Zndc를 1로 설정하고 A에 대해서 풀면 다음을 얻는다.
A(n/f-1)-n/f = 1
A(n/f-1) = 1 + n/f
A = (1 + n/f) / (n/f-1)
=(n+f)/(n-f)
B = (A-1)n 이 식에 대입하면
B = (2nf)/(n-f) 가 된다.
따라서 최종 행렬은
[ d/a 0 0 0 ]
[ 0 d 0 0 ]
[ 0 0 (n+f)/(n-f) 2nf/(n-f)]
[ 0 0 -1 0 ]
생성한 이 행렬은 OpenGL 함수 gluPerspective()를 호출함으로써 생성되는 행렬과 동일하다.
이 함수는 시야를 통해 시야,종횡비, 그리고 근단면과 원단면 설정을 인자로 받고 원근 행렬을
만들고 그것을 현재 행렬에 곱한다.
위에서 말했듯이 이는 OpengGL의 경우로 축약된다.
Directx는 z방향에 대해서 [0,1]로 사상한다.
[ d/a 0 0 0 ]
[ 0 d 0 0 ]
[ 0 0 f/(f-n) -nf/(f-n)]
[ 0 0 1 0 ]
컴퓨터 시스템의 y축과 수학적인 y축의 방향은 반대인것을 고려해야 한다.
http://medialab.di.unipi.it/web/IUM/Waterloo/node51.html
참고 : 게임&인터랙티브 애플리케이션을 위한 수학
[출처] DX 파이프라인 따라하기. [4. Projection 변환]-2 (비공개 카페)
'DirectX > 3D' 카테고리의 다른 글
| ASE 파서 파싱 (1) | 2010.07.27 |
|---|---|
| ASE 에니메이션을 하기위한 이론정리 (0) | 2010.07.26 |
| ASE 관련 서적 ASE 에니메이션 오브젝트 등등 (0) | 2010.07.19 |
| ASE 파일을 이용한 Bone Animation (1) (0) | 2010.07.19 |
| 픽킹~ 수학 이론 (0) | 2010.07.16 |
